Titanic Data Family Size and Chance of Survival Logistic Regression
Predicting the Survival of Titanic Passengers
![]()

In this weblog-post, I will go through the whole process of creating a automobile learning model on the famous Titanic dataset, which is used by many people all over the world. It provides information on the fate of passengers on the Titanic, summarized according to economical status (course), sexual activity, age and survival.
I initially wrote this postal service on kaggle.com, as part of the "Titanic: Car Learning from Disaster" Competition. In this challenge, nosotros are asked to predict whether a rider on the titanic would have been survived or not.
RMS Titanic
The RMS Titanic was a British passenger liner that sank in the North Atlantic Bounding main in the early morning hours of 15 April 1912, after it collided with an iceberg during its maiden voyage from Southampton to New York City. In that location were an estimated 2,224 passengers and crew aboard the ship, and more than 1,500 died, making it one of the deadliest commercial peacetime maritime disasters in modern history. The RMS Titanic was the largest ship afloat at the fourth dimension information technology entered service and was the 2nd of 3 Olympic-class ocean liners operated past the White Star Line. The Titanic was built by the Harland and Wolff shipyard in Belfast. Thomas Andrews, her architect, died in the disaster.

Importing the Libraries
# linear algebra
import numpy every bit np # data processing
import pandas as pd
# information visualization
import seaborn as sns
%matplotlib inline
from matplotlib import pyplot as plt
from matplotlib import style
# Algorithms
from sklearn import linear_model
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.naive_bayes import GaussianNB
Getting the Data
test_df = pd.read_csv("test.csv")
train_df = pd.read_csv("train.csv") Data Exploration/Analysis
train_df.info() 
The trainin g -gear up has 891 examples and 11 features + the target variable (survived). 2 of the features are floats, 5 are integers and 5 are objects. Beneath I have listed the features with a brusk clarification:
survival: Survival
PassengerId: Unique Id of a passenger.
pclass: Ticket class
sex: Sex
Age: Age in years
sibsp: # of siblings / spouses aboard the Titanic
parch: # of parents / children aboard the Titanic
ticket: Ticket number
fare: Passenger fare
motel: Cabin number
embarked: Port of Embarkation train_df.describe()

Above we can come across that 38% out of the grooming-set survived the Titanic. We can also see that the rider ages range from 0.iv to 80. On top of that we can already detect some features, that contain missing values, like the 'Historic period' characteristic.
train_df.caput(8) 
From the table above, we can note a few things. First of all, that we need to convert a lot of features into numeric ones subsequently on, so that the machine learning algorithms can process them. Furthermore, we tin come across that the features have widely different ranges, that we volition need to convert into roughly the same scale. We tin likewise spot some more than features, that contain missing values (NaN = not a number), that wee need to deal with.
Let's accept a more detailed look at what data is really missing:
total = train_df.isnull().sum().sort_values(ascending=Fake)
percent_1 = train_df.isnull().sum()/train_df.isnull().count()*100
percent_2 = (round(percent_1, i)).sort_values(ascending=Fake)
missing_data = pd.concat([total, percent_2], axis=1, keys=['Total', '%'])
missing_data.caput(v) 
The Embarked feature has simply 2 missing values, which tin can easily be filled. It will be much more tricky, to deal with the 'Historic period' feature, which has 177 missing values. The 'Cabin' feature needs further investigation, simply it looks similar that nosotros might want to driblet information technology from the dataset, since 77 % of it are missing.
train_df.columns.values 
Above you tin come across the 11 features + the target variable (survived). What features could contribute to a high survival rate ?
To me information technology would make sense if everything except 'PassengerId', 'Ticket' and 'Name' would be correlated with a high survival charge per unit.
1. Age and Sex:
survived = 'survived'
not_survived = 'non survived'
fig, axes = plt.subplots(nrows=ane, ncols=ii,figsize=(10, 4))
women = train_df[train_df['Sex']=='female']
men = train_df[train_df['Sex']=='male']
ax = sns.distplot(women[women['Survived']==one].Age.dropna(), bins=18, characterization = survived, ax = axes[0], kde =False)
ax = sns.distplot(women[women['Survived']==0].Historic period.dropna(), bins=forty, label = not_survived, ax = axes[0], kde =False)
ax.legend()
ax.set_title('Female')
ax = sns.distplot(men[men['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[1], kde = False)
ax = sns.distplot(men[men['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[1], kde = False)
ax.legend()
_ = ax.set_title('Male') 
You can meet that men have a high probability of survival when they are betwixt 18 and 30 years quondam, which is too a little chip true for women but not fully. For women the survival chances are higher between xiv and xl.
For men the probability of survival is very low betwixt the age of 5 and 18, but that isn't truthful for women. Another thing to note is that infants likewise have a little bit higher probability of survival.
Since there seem to be certain ages, which have increased odds of survival and because I want every feature to be roughly on the same scale, I will create age groups later on.
3. Embarked, Pclass and Sex activity:
FacetGrid = sns.FacetGrid(train_df, row='Embarked', size=4.v, aspect=1.vi)
FacetGrid.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', palette=None, order=None, hue_order=None )
FacetGrid.add_legend() 
Embarked seems to be correlated with survival, depending on the gender.
Women on port Q and on port South have a higher gamble of survival. The changed is true, if they are at port C. Men have a high survival probability if they are on port C, only a low probability if they are on port Q or South.
Pclass too seems to be correlated with survival. We will generate another plot of it beneath.
4. Pclass:
sns.barplot(ten='Pclass', y='Survived', information=train_df) 
Hither we see clearly, that Pclass is contributing to a persons gamble of survival, especially if this person is in grade 1. We will create another pclass plot below.
filigree = sns.FacetGrid(train_df, col='Survived', row='Pclass', size=ii.ii, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend(); 
The plot above confirms our supposition about pclass i, only we tin besides spot a loftier probability that a person in pclass iii volition not survive.
5. SibSp and Parch:
SibSp and Parch would brand more sense as a combined characteristic, that shows the full number of relatives, a person has on the Titanic. I will create it below and too a feature that sows if someone is not solitary.
data = [train_df, test_df]
for dataset in data:
dataset['relatives'] = dataset['SibSp'] + dataset['Parch']
dataset.loc[dataset['relatives'] > 0, 'not_alone'] = 0
dataset.loc[dataset['relatives'] == 0, 'not_alone'] = one
dataset['not_alone'] = dataset['not_alone'].astype(int) train_df['not_alone'].value_counts()

axes = sns.factorplot('relatives','Survived',
data=train_df, aspect = 2.5, ) 
Here we can meet that yous had a loftier probabilty of survival with 1 to 3 realitves, merely a lower ane if you had less than i or more than than iii (except for some cases with 6 relatives).
Data Preprocessing
Starting time, I volition drib 'PassengerId' from the train prepare, because it does non contribute to a persons survival probability. I will not drop it from the exam set up, since it is required there for the submission.
train_df = train_df.drop(['PassengerId'], axis=1) Missing Data:
Cabin:
Equally a reminder, nosotros have to deal with Motel (687), Embarked (2) and Age (177). Beginning I idea, we take to delete the 'Motel' variable just then I institute something interesting. A motel number looks like 'C123' and the alphabetic character refers to the deck. Therefore we're going to extract these and create a new feature, that contains a persons deck. Afterwords nosotros will convert the feature into a numeric variable. The missing values will exist converted to zero. In the film beneath you tin can come across the actual decks of the titanic, ranging from A to G.
import re
deck = {"A": 1, "B": 2, "C": 3, "D": 4, "East": 5, "F": 6, "Yard": vii, "U": viii}
information = [train_df, test_df]for dataset in data:
# we tin can now driblet the cabin characteristic
dataset['Cabin'] = dataset['Cabin'].fillna("U0")
dataset['Deck'] = dataset['Motel'].map(lambda x: re.compile("([a-zA-Z]+)").search(10).group())
dataset['Deck'] = dataset['Deck'].map(deck)
dataset['Deck'] = dataset['Deck'].fillna(0)
dataset['Deck'] = dataset['Deck'].astype(int)
train_df = train_df.drib(['Motel'], axis=1)
test_df = test_df.drop(['Motel'], axis=1)
Age:
At present nosotros tin can tackle the issue with the historic period features missing values. I will create an array that contains random numbers, which are computed based on the hateful historic period value in regards to the standard difference and is_null.
data = [train_df, test_df]for dataset in data:
train_df["Age"].isnull().sum()
mean = train_df["Historic period"].mean()
std = test_df["Age"].std()
is_null = dataset["Age"].isnull().sum()
# compute random numbers between the hateful, std and is_null
rand_age = np.random.randint(mean - std, hateful + std, size = is_null)
# fill NaN values in Age column with random values generated
age_slice = dataset["Historic period"].copy()
age_slice[np.isnan(age_slice)] = rand_age
dataset["Age"] = age_slice
dataset["Age"] = train_df["Age"].astype(int)

Embarked:
Since the Embarked characteristic has simply 2 missing values, we will just fill these with the about common one.
train_df['Embarked'].draw() 
common_value = 'S'
data = [train_df, test_df] for dataset in data:
dataset['Embarked'] = dataset['Embarked'].fillna(common_value)
Converting Features:
train_df.info() 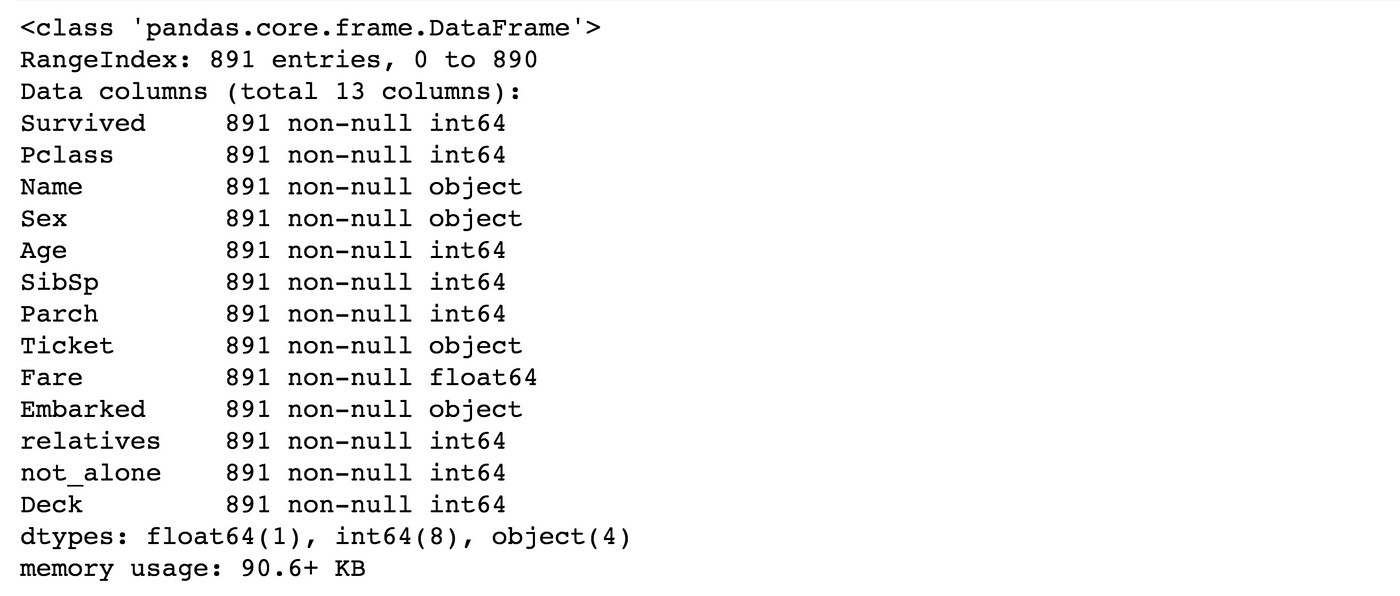
Above you lot tin can see that 'Fare' is a float and we take to bargain with iv categorical features: Name, Sexual activity, Ticket and Embarked. Lets investigate and transfrom one afterwards another.
Fare:
Converting "Fare" from bladder to int64, using the "astype()" role pandas provides:
information = [train_df, test_df] for dataset in data:
dataset['Fare'] = dataset['Fare'].fillna(0)
dataset['Fare'] = dataset['Fare'].astype(int)
Name:
We will use the Proper noun characteristic to excerpt the Titles from the Proper noun, so that we can build a new feature out of that.
data = [train_df, test_df]
titles = {"Mr": 1, "Miss": 2, "Mrs": 3, "Primary": iv, "Rare": five}for dataset in information:
train_df = train_df.driblet(['Name'], axis=ane)
# extract titles
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
# replace titles with a more common title or as Rare
dataset['Title'] = dataset['Title'].supervene upon(['Lady', 'Countess','Capt', 'Col','Don', 'Dr',\
'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].supplant('Mlle', 'Miss')
dataset['Championship'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Championship'].replace('Mme', 'Mrs')
# catechumen titles into numbers
dataset['Title'] = dataset['Title'].map(titles)
# filling NaN with 0, to get safe
dataset['Title'] = dataset['Title'].fillna(0)
test_df = test_df.drop(['Name'], axis=1)
Sex:
Convert 'Sexual activity' feature into numeric.
genders = {"male": 0, "female": i}
data = [train_df, test_df] for dataset in data:
dataset['Sex'] = dataset['Sex activity'].map(genders)
Ticket:
train_df['Ticket'].describe() 
Since the Ticket aspect has 681 unique tickets, it volition exist a bit catchy to convert them into useful categories. And so nosotros will drib it from the dataset.
train_df = train_df.drop(['Ticket'], axis=1)
test_df = test_df.drop(['Ticket'], axis=ane) Embarked:
Convert 'Embarked' feature into numeric.
ports = {"S": 0, "C": 1, "Q": ii}
information = [train_df, test_df] for dataset in information:
dataset['Embarked'] = dataset['Embarked'].map(ports)
Creating Categories:
We will at present create categories within the following features:
Age:
Now we need to convert the 'age' feature. First we will convert information technology from float into integer. Then we will create the new 'AgeGroup" variable, past categorizing every age into a group. Note that it is important to place attention on how you form these groups, since yous don't want for example that lxxx% of your data falls into group 1.
information = [train_df, test_df]
for dataset in data:
dataset['Age'] = dataset['Age'].astype(int)
dataset.loc[ dataset['Age'] <= 11, 'Historic period'] = 0
dataset.loc[(dataset['Historic period'] > 11) & (dataset['Historic period'] <= 18), 'Age'] = i
dataset.loc[(dataset['Age'] > xviii) & (dataset['Historic period'] <= 22), 'Historic period'] = 2
dataset.loc[(dataset['Age'] > 22) & (dataset['Age'] <= 27), 'Age'] = 3
dataset.loc[(dataset['Age'] > 27) & (dataset['Age'] <= 33), 'Age'] = 4
dataset.loc[(dataset['Age'] > 33) & (dataset['Age'] <= twoscore), 'Historic period'] = five
dataset.loc[(dataset['Historic period'] > forty) & (dataset['Age'] <= 66), 'Age'] = 6
dataset.loc[ dataset['Age'] > 66, 'Age'] = 6
# let'south see how it's distributed train_df['Historic period'].value_counts() 
Fare:
For the 'Fare' characteristic, we demand to practice the aforementioned every bit with the 'Historic period' feature. But it isn't that piece of cake, considering if we cut the range of the fare values into a few as big categories, fourscore% of the values would fall into the first category. Fortunately, we can employ sklearn "qcut()" role, that nosotros can use to see, how we can form the categories.
train_df.caput(10) 
information = [train_df, test_df] for dataset in information:
dataset.loc[ dataset['Fare'] <= seven.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = ane
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[(dataset['Fare'] > 31) & (dataset['Fare'] <= 99), 'Fare'] = 3
dataset.loc[(dataset['Fare'] > 99) & (dataset['Fare'] <= 250), 'Fare'] = 4
dataset.loc[ dataset['Fare'] > 250, 'Fare'] = 5
dataset['Fare'] = dataset['Fare'].astype(int)
Creating new Features
I will add together two new features to the dataset, that I compute out of other features.
i. Age times Course
data = [train_df, test_df]
for dataset in information:
dataset['Age_Class']= dataset['Age']* dataset['Pclass'] 2. Fare per Person
for dataset in data:
dataset['Fare_Per_Person'] = dataset['Fare']/(dataset['relatives']+1)
dataset['Fare_Per_Person'] = dataset['Fare_Per_Person'].astype(int) # Allow's take a last look at the preparation prepare, earlier we start training the models.
train_df.head(10)

Edifice Motorcar Learning Models
Now we volition train several Machine Learning models and compare their results. Note that considering the dataset does not provide labels for their testing-set, nosotros need to utilize the predictions on the training set up to compare the algorithms with each other. Later on, we will use cross validation.
X_train = train_df.drop("Survived", centrality=i)
Y_train = train_df["Survived"]
X_test = test_df.driblet("PassengerId", axis=one).copy() Stochastic Gradient Descent (SGD):
sgd = linear_model.SGDClassifier(max_iter=5, tol=None)
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)sgd.score(X_train, Y_train)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, ii)
Random Forest:
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
Logistic Regression:
logreg = LogisticRegression()
logreg.fit(X_train, Y_train)Y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)
K Nearest Neighbor:
# KNN knn = KNeighborsClassifier(n_neighbors = iii) knn.fit(X_train, Y_train) Y_pred = knn.predict(X_test) acc_knn = circular(knn.score(X_train, Y_train) * 100, 2) Gaussian Naive Bayes:
gaussian = GaussianNB() gaussian.fit(X_train, Y_train) Y_pred = gaussian.predict(X_test) acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2) Perceptron:
perceptron = Perceptron(max_iter=5)
perceptron.fit(X_train, Y_train)Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, ii)
Linear Back up Vector Machine:
linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, ii)
Conclusion Tree
decision_tree = DecisionTreeClassifier() decision_tree.fit(X_train, Y_train) Y_pred = decision_tree.predict(X_test) acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2) Which is the best Model ?
results = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Stochastic Slope Decent',
'Conclusion Tree'],
'Score': [acc_linear_svc, acc_knn, acc_log,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_sgd, acc_decision_tree]})
result_df = results.sort_values(past='Score', ascending=Fake)
result_df = result_df.set_index('Score')
result_df.caput(9) 
As we tin can see, the Random Woods classifier goes on the outset place. But starting time, let u.s.a. check, how random-forest performs, when we use cantankerous validation.
K-Fold Cantankerous Validation:
K-Fold Cross Validation randomly splits the training information into K subsets chosen folds. Allow'south image we would split our data into 4 folds (K = 4). Our random forest model would exist trained and evaluated four times, using a different fold for evaluation everytime, while it would be trained on the remaining 3 folds.
The image below shows the process, using 4 folds (K = iv). Every row represents one grooming + evaluation procedure. In the first row, the model become's trained on the get-go, 2d and third subset and evaluated on the fourth. In the second row, the model go's trained on the second, third and fourth subset and evaluated on the first. Thou-Fold Cross Validation repeats this procedure till every fold acted once as an evaluation fold.

The effect of our K-Fold Cross Validation example would be an array that contains 4 different scores. We then need to compute the mean and the standard deviation for these scores.
The code below perform 1000-Fold Cross Validation on our random forest model, using ten folds (K = 10). Therefore it outputs an array with 10 unlike scores.
from sklearn.model_selection import cross_val_score
rf = RandomForestClassifier(n_estimators=100)
scores = cross_val_score(rf, X_train, Y_train, cv=10, scoring = "accuracy") print("Scores:", scores)
print("Mean:", scores.mean())
print("Standard Divergence:", scores.std())

This looks much more than realistic than before. Our model has a average accuracy of 82% with a standard deviation of 4 %. The standard divergence shows us, how precise the estimates are .
This ways in our case that the accuracy of our model can differ + — 4%.
I think the accuracy is still really practiced and since random woods is an easy to use model, we will try to increment it'south performance even further in the following section.
Random Woods
What is Random Forest ?
Random Forest is a supervised learning algorithm. Like you can already meet from it's name, it creates a forest and makes information technology somehow random. The „forest" it builds, is an ensemble of Determination Trees, most of the time trained with the "bagging" method. The general idea of the bagging method is that a combination of learning models increases the overall event.
To say it in simple words: Random woods builds multiple conclusion trees and merges them together to become a more accurate and stable prediction.
One big advantage of random forest is, that information technology tin can exist used for both classification and regression problems, which form the majority of current machine learning systems. With a few exceptions a random-forest classifier has all the hyperparameters of a decision-tree classifier and likewise all the hyperparameters of a bagging classifier, to control the ensemble itself.
The random-forest algorithm brings extra randomness into the model, when it is growing the trees. Instead of searching for the best feature while splitting a node, it searches for the best feature among a random subset of features. This procedure creates a wide variety, which more often than not results in a better model. Therefore when you are growing a tree in random forest, only a random subset of the features is considered for splitting a node. Yous can even make trees more random, by using random thresholds on elevation of it, for each feature rather than searching for the best possible thresholds (like a normal decision tree does).
Below you tin see how a random forest would look similar with two trees:
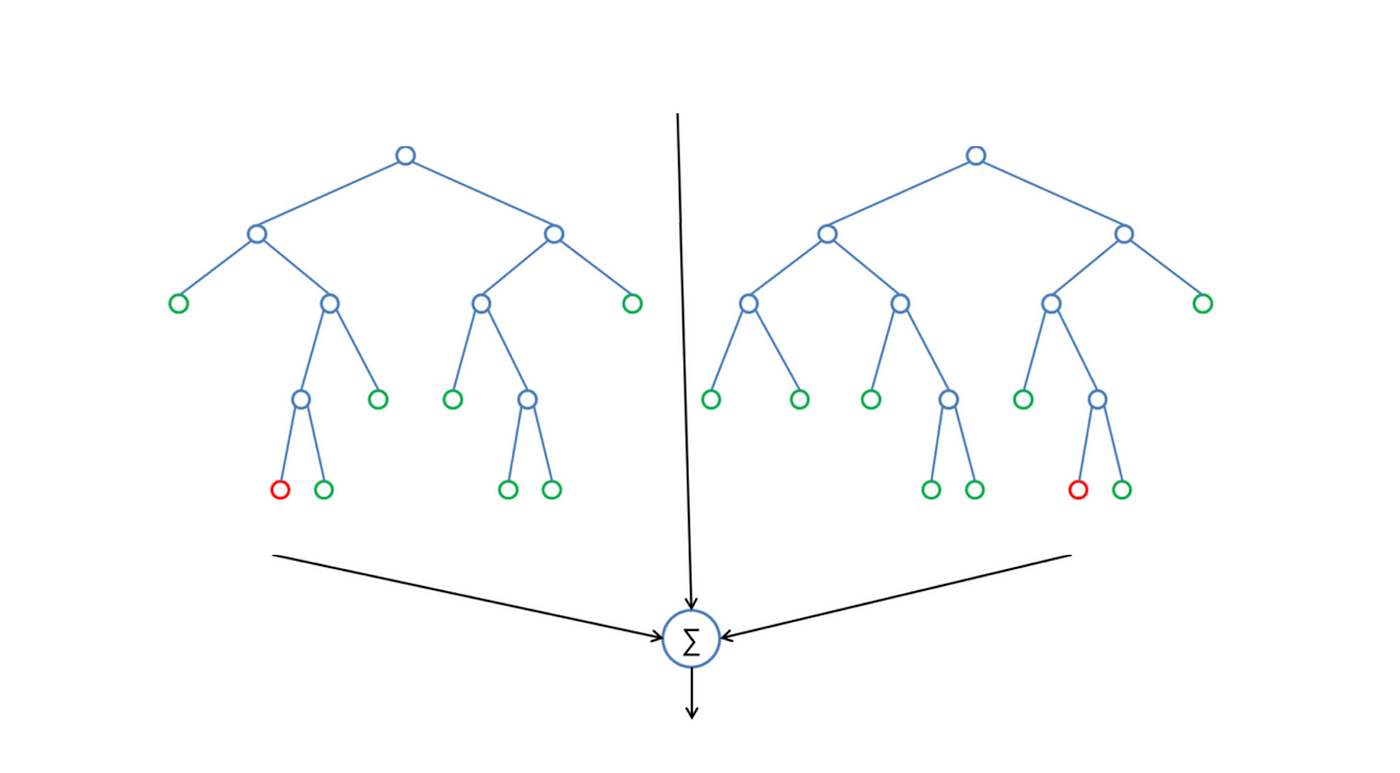
Feature Importance
Some other great quality of random forest is that they brand it very easy to measure the relative importance of each characteristic. Sklearn measure a features importance by looking at how much the treee nodes, that employ that characteristic, reduce impurity on average (across all trees in the forest). Information technology computes this score automaticall for each feature after preparation and scales the results so that the sum of all importances is equal to ane. We will acces this below:
importances = pd.DataFrame({'characteristic':X_train.columns,'importance':np.round(random_forest.feature_importances_,3)})
importances = importances.sort_values('importance',ascending=False).set_index('feature') importances.caput(15)

importances.plot.bar() 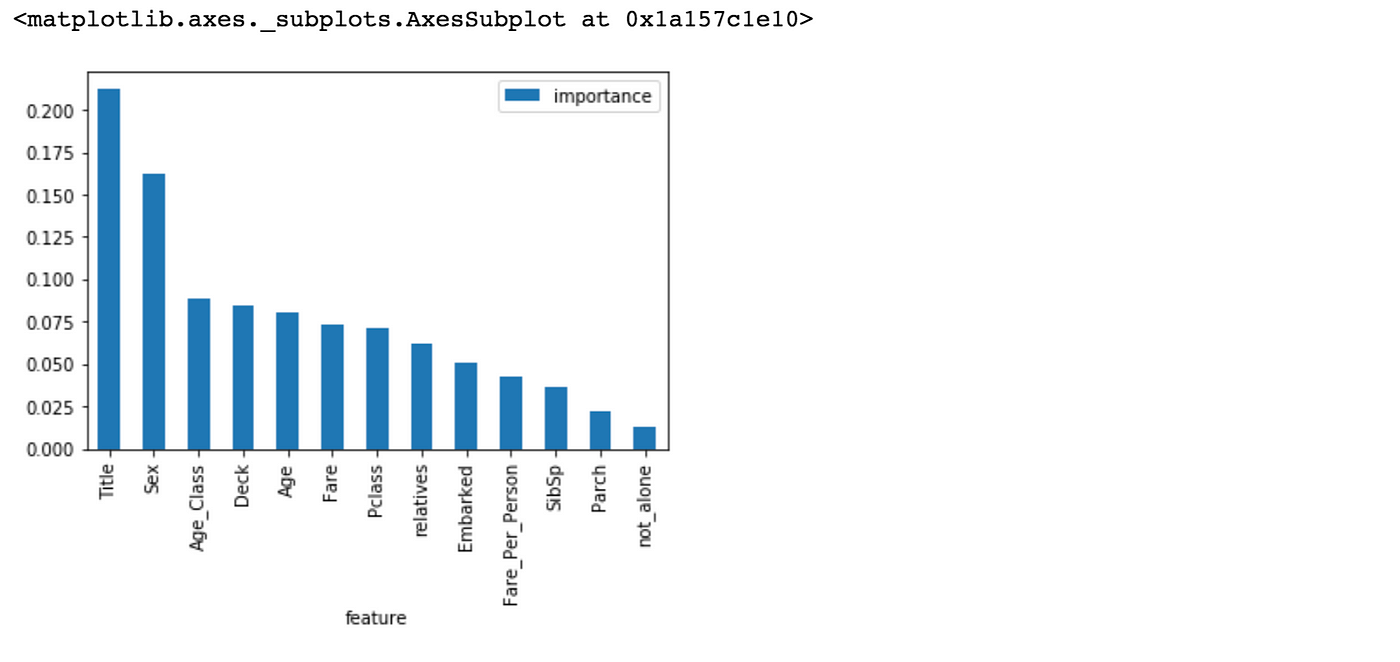
Decision:
not_alone and Parch doesn't play a significant part in our random forest classifiers prediction process. Because of that I will drop them from the dataset and train the classifier again. We could likewise remove more or less features, but this would need a more detailed investigation of the features effect on our model. But I recollect it'south but fine to remove simply Alone and Parch.
train_df = train_df.drop("not_alone", axis=one)
test_df = test_df.drop("not_alone", centrality=one)train_df = train_df.drop("Parch", axis=1)
test_df = test_df.drop("Parch", axis=1)
Preparation random woods over again:
# Random Forest random_forest = RandomForestClassifier(n_estimators=100, oob_score = Truthful)
random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
print(round(acc_random_forest,2,), "%")
92.82%
Our random forest model predicts equally adept as it did before. A full general dominion is that, the more features you have, the more than likely your model will suffer from overfitting and vice versa. Merely I recollect our data looks fine for now and hasn't as well much features.
In that location is also another style to evaluate a random-forest classifier, which is probably much more accurate than the score nosotros used earlier. What I am talking almost is the out-of-bag samples to estimate the generalization accuracy. I will not go into details hither about how information technology works. Just note that out-of-handbag estimate is as accurate as using a test fix of the same size as the training set. Therefore, using the out-of-bag error estimate removes the demand for a fix bated test set.
print("oob score:", round(random_forest.oob_score_, four)*100, "%") oob score: 81.82 %
Now we can start tuning the hyperameters of random forest.
Hyperparameter Tuning
Below you tin see the lawmaking of the hyperparamter tuning for the parameters benchmark, min_samples_leaf, min_samples_split and n_estimators.
I put this lawmaking into a markdown prison cell and not into a lawmaking prison cell, considering information technology takes a long time to run it. Direct underneeth information technology, I put a screenshot of the gridsearch's output.
param_grid = { "criterion" : ["gini", "entropy"], "min_samples_leaf" : [1, v, 10, 25, 50, 70], "min_samples_split" : [2, iv, ten, 12, xvi, 18, 25, 35], "n_estimators": [100, 400, 700, 1000, 1500]} from sklearn.model_selection import GridSearchCV, cross_val_score rf = RandomForestClassifier(n_estimators=100, max_features='auto', oob_score=True, random_state=1, n_jobs=-1) clf = GridSearchCV(calculator=rf, param_grid=param_grid, n_jobs=-ane) clf.fit(X_train, Y_train) clf.bestparams

Examination new Parameters:
# Random Forest
random_forest = RandomForestClassifier(criterion = "gini",
min_samples_leaf = 1,
min_samples_split = 10,
n_estimators=100,
max_features='auto',
oob_score=True,
random_state=1,
n_jobs=-1)random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
impress("oob score:", round(random_forest.oob_score_, iv)*100, "%")
oob score: 83.05 %
Now that we accept a proper model, we can start evaluating it'due south performace in a more authentic way. Previously we but used accuracy and the oob score, which is just another grade of accuracy. The problem is but, that it's more complicated to evaluate a nomenclature model than a regression model. We will talk most this in the following section.
Further Evaluation
Confusion Matrix:
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
predictions = cross_val_predict(random_forest, X_train, Y_train, cv=iii)
confusion_matrix(Y_train, predictions) 
The first row is most the not-survived-predictions: 493 passengers were correctly classified equally not survived (called true negatives) and 56 where wrongly classified as non survived (faux positives).
The second row is about the survived-predictions: 93 passengers where wrongly classified as survived (fake negatives) and 249 where correctly classified as survived (true positives).
A confusion matrix gives you a lot of data nigh how well your model does, but theres a way to become even more, like computing the classifiers precision.
Precision and Call back:
from sklearn.metrics import precision_score, recall_scoreprint("Precision:", precision_score(Y_train, predictions))
print("Call back:",recall_score(Y_train, predictions))
Precision: 0.801948051948
Call back: 0.722222222222
Our model predicts 81% of the fourth dimension, a passengers survival correctly (precision). The call up tells usa that it predicted the survival of 73 % of the people who really survived.
F-Score
You can combine precision and recall into one score, which is called the F-score. The F-score is computed with the harmonic mean of precision and recall. Annotation that information technology assigns much more weight to low values. Every bit a issue of that, the classifier will only get a high F-score, if both recall and precision are loftier.
from sklearn.metrics import f1_score
f1_score(Y_train, predictions) 0.7599999999999
There we take it, a 77 % F-score. The score is non that high, considering we have a recall of 73%. But unfortunately the F-score is not perfect, because it favors classifiers that have a similar precision and remember. This is a trouble, because you sometimes want a high precision and sometimes a loftier recall. The thing is that an increasing precision, sometimes results in an decreasing recall and vice versa (depending on the threshold). This is called the precision/recall tradeoff. We will hash out this in the post-obit section.
Precision Recall Curve
For each person the Random Forest algorithm has to classify, information technology computes a probability based on a function and it classifies the person equally survived (when the score is bigger the than threshold) or as not survived (when the score is smaller than the threshold). That's why the threshold plays an important part.
We volition plot the precision and recall with the threshold using matplotlib:
from sklearn.metrics import precision_recall_curve# getting the probabilities of our predictions
y_scores = random_forest.predict_proba(X_train)
y_scores = y_scores[:,1]precision, recall, threshold = precision_recall_curve(Y_train, y_scores)
def plot_precision_and_recall(precision, recall, threshold):
plt.plot(threshold, precision[:-1], "r-", characterization="precision", linewidth=five)
plt.plot(threshold, call back[:-1], "b", label="recall", linewidth=5)
plt.xlabel("threshold", fontsize=19)
plt.legend(loc="upper right", fontsize=xix)
plt.ylim([0, 1])plt.effigy(figsize=(14, 7))
plot_precision_and_recall(precision, retrieve, threshold)
plt.testify()

To a higher place you can clearly see that the recall is falling of rapidly at a precision of effectually 85%. Because of that you may want to select the precision/recall tradeoff earlier that — maybe at around 75 %.
You are now able to cull a threshold, that gives y'all the best precision/call up tradeoff for your current car learning problem. If you desire for example a precision of 80%, you can easily look at the plots and run across that you would demand a threshold of effectually 0.4. And so you could train a model with exactly that threshold and would get the desired accurateness.
Some other way is to plot the precision and recall against each other:
def plot_precision_vs_recall(precision, retrieve):
plt.plot(call up, precision, "thousand--", linewidth=two.5)
plt.ylabel("recall", fontsize=19)
plt.xlabel("precision", fontsize=19)
plt.axis([0, one.five, 0, 1.5])plt.figure(figsize=(14, 7))
plot_precision_vs_recall(precision, recollect)
plt.show()

ROC AUC Bend
Some other manner to evaluate and compare your binary classifier is provided by the ROC AUC Curve. This bend plots the true positive charge per unit (also chosen retrieve) against the fake positive rate (ratio of incorrectly classified negative instances), instead of plotting the precision versus the recall.
from sklearn.metrics import roc_curve
# compute true positive rate and false positive rate
false_positive_rate, true_positive_rate, thresholds = roc_curve(Y_train, y_scores) # plotting them against each other
def plot_roc_curve(false_positive_rate, true_positive_rate, characterization=None):
plt.plot(false_positive_rate, true_positive_rate, linewidth=ii, label=label)
plt.plot([0, 1], [0, 1], 'r', linewidth=four)
plt.axis([0, one, 0, 1])
plt.xlabel('False Positive Rate (FPR)', fontsize=16)
plt.ylabel('True Positive Rate (TPR)', fontsize=16)plt.effigy(figsize=(14, 7))
plot_roc_curve(false_positive_rate, true_positive_rate)
plt.show()
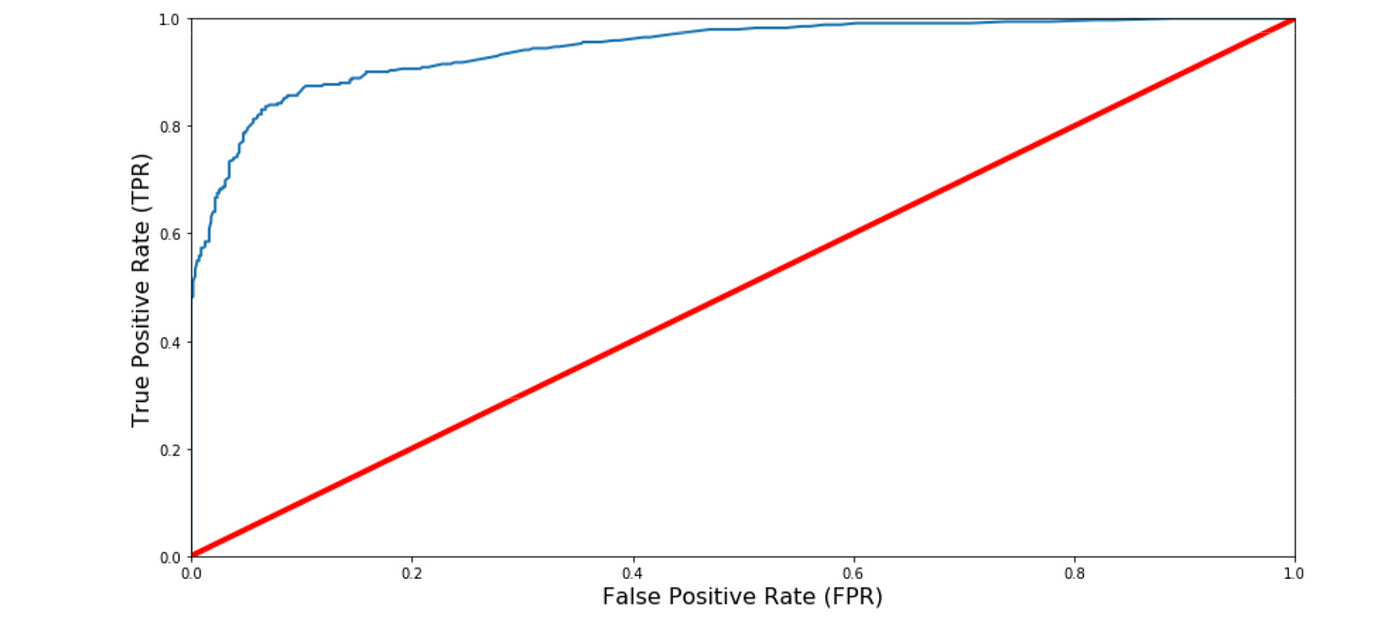
The red line in the middel represents a purely random classifier (e.yard a coin flip) and therefore your classifier should be as far away from it equally possible. Our Random Forest model seems to practise a adept task.
Of course we also have a tradeoff here, considering the classifier produces more false positives, the higher the true positive rate is.
ROC AUC Score
The ROC AUC Score is the corresponding score to the ROC AUC Curve. Information technology is simply computed by measuring the area nether the curve, which is chosen AUC.
A classifiers that is 100% correct, would take a ROC AUC Score of 1 and a completely random classiffier would take a score of 0.v.
from sklearn.metrics import roc_auc_score
r_a_score = roc_auc_score(Y_train, y_scores)
impress("ROC-AUC-Score:", r_a_score) ROC_AUC_SCORE: 0.945067587
Nice ! I call back that score is good enough to submit the predictions for the examination-set to the Kaggle leaderboard.
Summary
We started with the data exploration where we got a feeling for the dataset, checked about missing information and learned which features are of import. During this procedure we used seaborn and matplotlib to do the visualizations. During the data preprocessing part, we computed missing values, converted features into numeric ones, grouped values into categories and created a few new features. Subsequently we started training 8 different machine learning models, picked one of them (random woods) and applied cross validation on it. Then we discussed how random woods works, took a wait at the importance it assigns to the different features and tuned information technology's performace through optimizing it's hyperparameter values. Lastly, we looked at it's defoliation matrix and computed the models precision, recall and f-score.
Below you tin can see a earlier and later on flick of the "train_df" dataframe:

Of course there is still room for improvement, like doing a more all-encompassing feature engineering, past comparing and plotting the features against each other and identifying and removing the noisy features. Another thing that can amend the overall effect on the kaggle leaderboard would exist a more extensive hyperparameter tuning on several machine learning models. You could also practice some ensemble learning.
Source: https://towardsdatascience.com/predicting-the-survival-of-titanic-passengers-30870ccc7e8
0 Response to "Titanic Data Family Size and Chance of Survival Logistic Regression"
Post a Comment